3. Modelling cyclone hazard in Bangladesh
This exercise deals with the use of GIS for cyclone hazard zonation, in a study area South of Chittagong, Bangladesh, using data of the April 1991 cyclone. The exercise will produce several maps of the expected number of casualties per village and population category caused by cyclone flood events with return periods of 5, 10, 20 and 50 years. Prior to this, maps have to be made of the flood depth per return period, the population density and the vulnerability of the population to flooding. For the calculation of the flood depths, use will be made of a digital terrain model and a linear flood-decay model.
Introduction
Despite the fact that the Bangladesh Government issued warnings of the impending flooding for the April 1991 cyclone, and about 3 million people could have been moved to safety, many inhabitants remained behind to protect their property.
During this disaster an estimated 138.000 people were killed and large numbers of houses, agricultural lands and infra-structural works were destroyed. Hundreds of schools were damaged and seven to eight thousand vessels were lost. Almost every bridge and culvert in the area was damaged and roads were washed out.
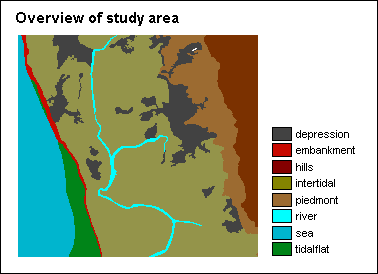
The Banskhali study area is situated in the East of Bangladesh, South of the city of Chittagong. Area maps and attribute tables of the geomorphology, village population, the Union-districts, roads, embankments, cyclone shelters, and the elevation of the terrain with cm accuracy are provided. Also available are a Landsat Thematic Mapper and SPOT panchromatic image. For a general introduction you can make use of a geomorphologic overview map of the whole coastal zone of Bangladesh as well as ten ground photographs of the Banskhali area.
The map view above gives an overview of the study area; two pictures taken in the area are shown below, the first picture was taken along the embankment, the second was taken at the river side.
First picture: Dike destroyed by local population for house construction. Second picture: Bamboo bridge over the river.
- You start by opening various maps, images and tables to get familiar with the study area. A number of polygon and segment maps have to be rasterized.
- Optionally you can create a DEM by performing an interpolation between points with height information.
- Furthermore, you create a number of graphs from the table with cyclone information to determine relations between wind speed, tidal height, surge height and number of casualties.
Cyclone flood modelling
In this application, surge heights are modelled as follows:
- the surge height remains constant for a certain distance from the coast line,
- then, the surge height decreases according to a constant factor, the so-called Surge Decay Coefficient (SDC); this is the influence of resistance caused by surface forms and land cover,
- at a certain distance from the coast the surge height will be zero.
The SDC is calculated as:
Surge height - Average elevation at end of surge
----------------------------------------------
Total inundation width - Width of constant surge
The picture below shows an example for a surge height of 650cm at the coast line.
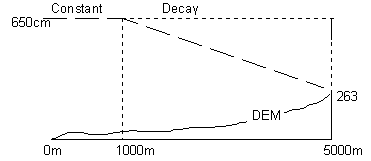
For a surge height of 650cm at the coast, you will calculate a flood hazard map which depicts the water height (in cm) in the area (all required parameters are given):
- first you will perform a distance calculation from the coast line,
- and with various MapCalc formulas using the Surge Decay Coefficient, you will obtain a map with the water height (in cm) in the area after the surge of 650cm.
The map to the right shows the result; for a better overview, the boundaries of sub-districts were overlaid. See that the highest water levels are reached in the South-West of the area.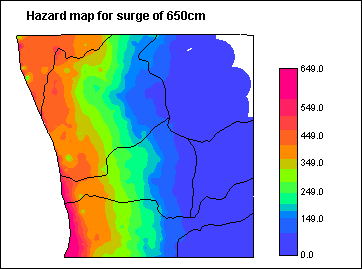
Modelling other surge levels
The SDC factors for surge heights of 370cm, 410cm, 470cm and 510cm need to be calculated. From the text of the application, you can find the total inundation widths and the widths of the areas under constant surge.
To find the average elevation at the end of the inundations, you will first use MapCalc to create special elevation maps. These elevation maps only contain the elevation at the end of the total inundation width for each of the above surge heights. You will then calculate histograms of these maps and by using the weighted average function, you will find the average elevation at the end of the inundations.
When SDC factors and other variables are known, you will use a pre-processed script for the automatic calculation of flood hazard maps for all surge heights.
The hazard patterns in the output maps are similar to the hazard map for a surge height of 650cm; water levels are of course less high in the maps with smaller surge heights.
Vulnerability and risk analysis
The vulnerability of the people to flooding is the degree of the population that will die as a result of flooding. The highest loss of people (factor 1.0) will occur at places where high flood depths occur, while there will be no loss of people (factor 0.0) at places where the flood depth is zero. (In this exercise, vulnerability is regarded as a kind of 'killing factor'.)
Literature provides the following information on the April 1991 cyclone in the Chittagong area:
- Casualty figures in several of the villages near the coast were as high as 70 percent of the population.
- In a belt at some distance from the coast, but still in the hazard zone, the casualty rate was in the range of 30-35 percent.
- In the whole coastal belt, including the areas at the foot of the hills outside the hazard zone, deaths were probably up to 20-30 percent of the existing population.
- The casualty rates for the different population categories were as follows: Children: 50%, Women: 25%. Elderly: 15% and Men: 10%
To find the degree of population loss for any flood depth, first so-called vulnerability coefficients are calculated. When these factors are multiplied with the flood depth values in the hazard map, you obtain a map in which every pixel has a value between 0.0 and 1.0 representing the loss of people for that pixel. You will do this for various surge heights by running another script, each time using the corresponding hazard map as input.
You will do this for various surge heights by running another script, each time using the corresponding hazard map as input.
Calculation of population densities
Population densities are calculated per village in table Village.
When calculating the total population density, you need to keep in mind that 16% of the population will flee to safer places and are thus assumed unaffected.
Densities are also calculated for different categories of the population: children, elderly, men and women.
From the resulting population density columns, attribute maps are derived.
Calculation of the number of casualties per village
For every surge height, maps depicting the number of casualties per village are calculated by multiplying the population density maps with the vulnerability maps (where the latter are the degree of people that will probably be killed for a certain surge height).
The casualty maps are expressed in number of people per ha per village that will drown as a result of a certain surge height flooding.
You will calculate the total loss of population, as well as population losses in the different population categories (children, women, elderly and men).
For population categories losses, extra multiplication factors are used representing the susceptibility of a category to drowning as a result of flooding: for children: 50% ; for women: 25% ; for elderly: 15% ; for men: 10%.
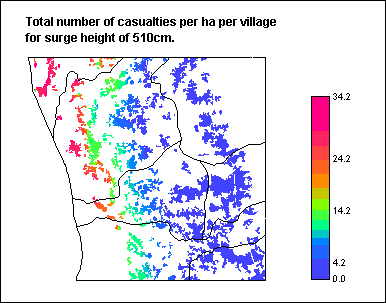
The map on the right presents the total number of casualties per ha per village for the 510cm surge height.
See that although hazards were found very large in the south-western part of the area, there are actually no villages in that part and most casualties are observed in the north-western part of the study area.
Subsequently, you will calculate new population densities for 50 and 100 years from now, assuming a population growth rate of 2.5%, and an increase of the village area of 25% in 50 years and 50% after 100 years. Then new casualty maps are calculated in the same way as before.
The new casualty maps show the same pattern as the previous ones, only that the number of casualties has increased dramatically.
Calculation of risk
Finally, to make some predictions on risks during next 100 years, risk maps are calculated as:
Probability of occurrence in 100 y * Vulnerability * Population density
The calculation of risks is done separately for the total population, for the population categories and for surge heights expected every 50 years, 20 years, 10 years and 5 years.
The risk calculations do not not take population growth into account and the different surge height risks are not summed into one 100y risk map.
In general, it can be concluded that small surge heights (=cyclones that occur more often) result in higher risks and within the population categories, the children's category has the highest risk and the elderly category the lowest. The risks within population categories however are entirely dependent on the category densities.
Note: when comparing maps of different return times or of different population categories, it is highly recommended to stretch the maps using the same maximum value.
For information on this case study, contact:
M.C.J. Damen and C.J. van Westen
Department of Earth Systems Analysis,
International Institute for Geo-Information Science and Earth Observation (ITC),
P.O. Box 6, 7500 AA Enschede, The Netherlands.
Tel: +31 53 4874266, Fax: +31 53 4874336, e-mail: damen@itc.nl
Tel: +31 53 4874263, Fax: +31 53 4874336, e-mail: westen@itc.nl